Vertex of a Parabola
| Main Concept | | The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry. For a parabola whose equation is given in standard form , the vertex will be the minimum (lowest point) of the graph if and the maximum (highest point) of the graph if .  | Vertex form | | The vertex form of a parabola is where is the vertex. The variable has the same value and function as the variable in the standard form. If (positive) the parabola opens up, and if (negative) the parabola opens down. The vertex form of a parabola is usually not provided. To convert from the standard form to vertex form, you must complete the square.  | Example of completing the square: | | | 1. Factor the leading coefficient out of the first two terms. | | | | 2. Complete the square by addition and subtracting the magic number - the square of half the coefficient of . | | | | 3. Factor out the constant . | | | | 4. Factor the perfect square. | | | | | | | | |
|
Use the sliders to change the vertex and observe how your changes affect the graph of the parabola.
Observe that when the graph opens up, the range of the corresponding quadratic function is , while if it opens down, the range is .
| Value of 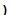 | | Value of :  | | | Value of :  | | |
|
| More MathApps | | MathApps/FunctionsAndRelations MathApps/Graphing | |
|
how to find the vertex of a parabola
Source: https://www.maplesoft.com/support/help/maple/view.aspx?path=MathApps%2FVertexOfAParabola
Posted by: campbellsplad1984.blogspot.com




0 Response to "how to find the vertex of a parabola"
Post a Comment